Prerequisites

Load the libraries with R:

library(astsa)

Section example: CO2 data

Time series data are data points collected over a period of time as a sequence of time gap. Time series data analysis means analyzing the available data to find out the pattern or trend in the data to predict some future values which will, in turn, help more effective and optimize decisions. Time series analysis examples are Financial, Stock prices, Weather data, Utility Studies and many more.

Let’s use the ‘Keeling_Data’ CO2 data again as an example to take a closer look at a time series.

# Read data
Keeling_Data     <- read.csv(file = "co2_mm_mlo.csv", header = T)

# Handel missing values
Keeling_Data$co2[which(Keeling_Data$co2<0)] <- NA

for(i in 1:length(Keeling_Data$co2)){
  if( is.na(Keeling_Data$co2[i])){
    Keeling_Data$co2[i] <- mean(Keeling_Data$co2[(i-2):(i+2)],na.rm=T )
  }
}

Notice that here we use 5-month average to replace the missing values.

Use ts() to convert a vector into a time series. Use ? to learn more.

# Apply the ts() function
co2 <- ts(Keeling_Data$co2, start=c(1958,3), frequency=12)

# Quick plot
plot(co2, type="l")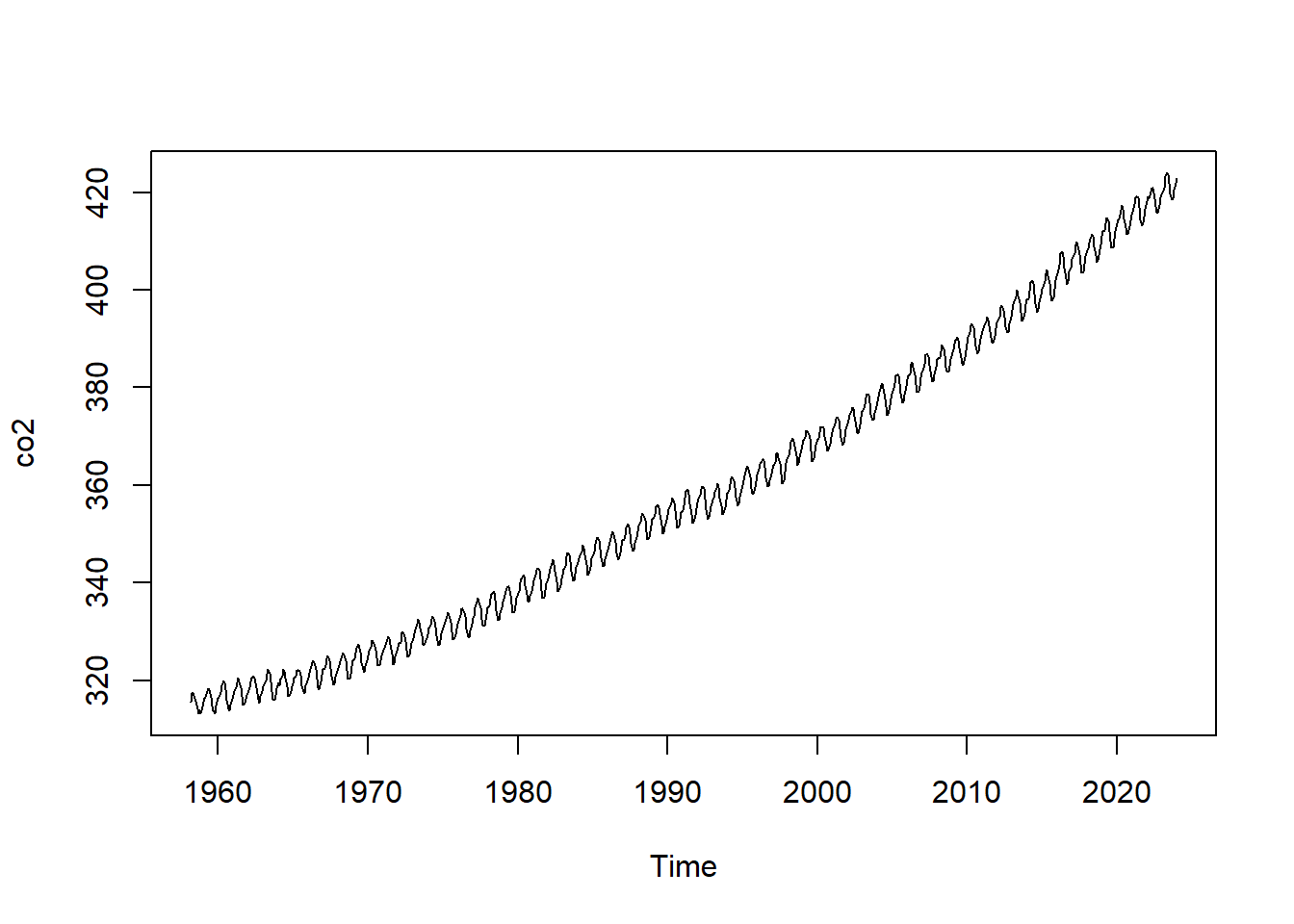

# Check the data type
str(co2)
##  Time-Series [1:791] from 1958 to 2024: 316 317 318 316 316 ...

Quick look: components of a time series

Generally, an environmental time series, \(Y(t)\), has three components: trend \(T(t)\), seasonality (e.g., 12-month cycle) \(S(t)\), and error \(e(t)\).

\[ Y(t) = T(t) + S(t) + e(t)\] Here the error \(e(t)\) part is called white noise. A white noise (\(w_t\)) is a collection of uncorrelated random variables with mean 0 and finite variance, denoted as: \[w_t \sim wn(0,\sigma^2)\]

In R, you can use decompose() to quickly decompose a time series into the three components, particularly for environmental data set. Here is how it works:

  • The function first determines the trend component using a moving average (if filter is NULL, a symmetric window with equal weights is used), and removes it from the time series.

  • Then, the seasonal figure is computed by averaging, for each time unit, over all periods. The seasonal figure is then centered.

  • Finally, the error component is determined by removing trend and seasonal figure (recycled as needed) from the original time series.

co2_components <- decompose(co2)
plot(co2_components)

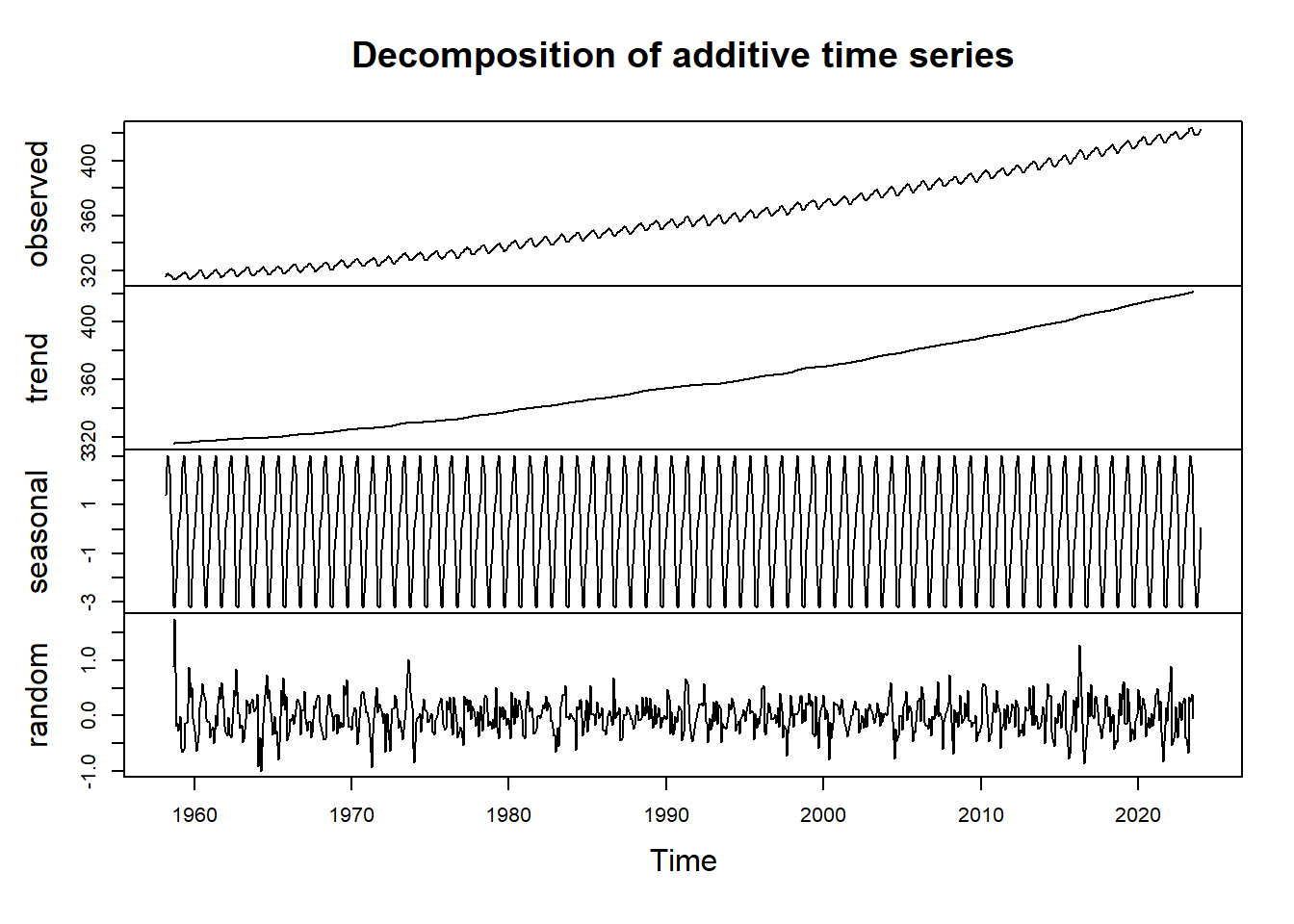
In the above example, co2_components contains the information/values of the three components. Check the distribution of the error component (random) to verify it’s a white noise.

# Plot hist
hist(co2_components$random, prob=TRUE)

# Add a normal pdf curve
curve(dnorm(x, mean=mean(co2_components$random, na.rm=T),
            sd=sd(co2_components$random, na.rm=T)),
      add=TRUE, col="red")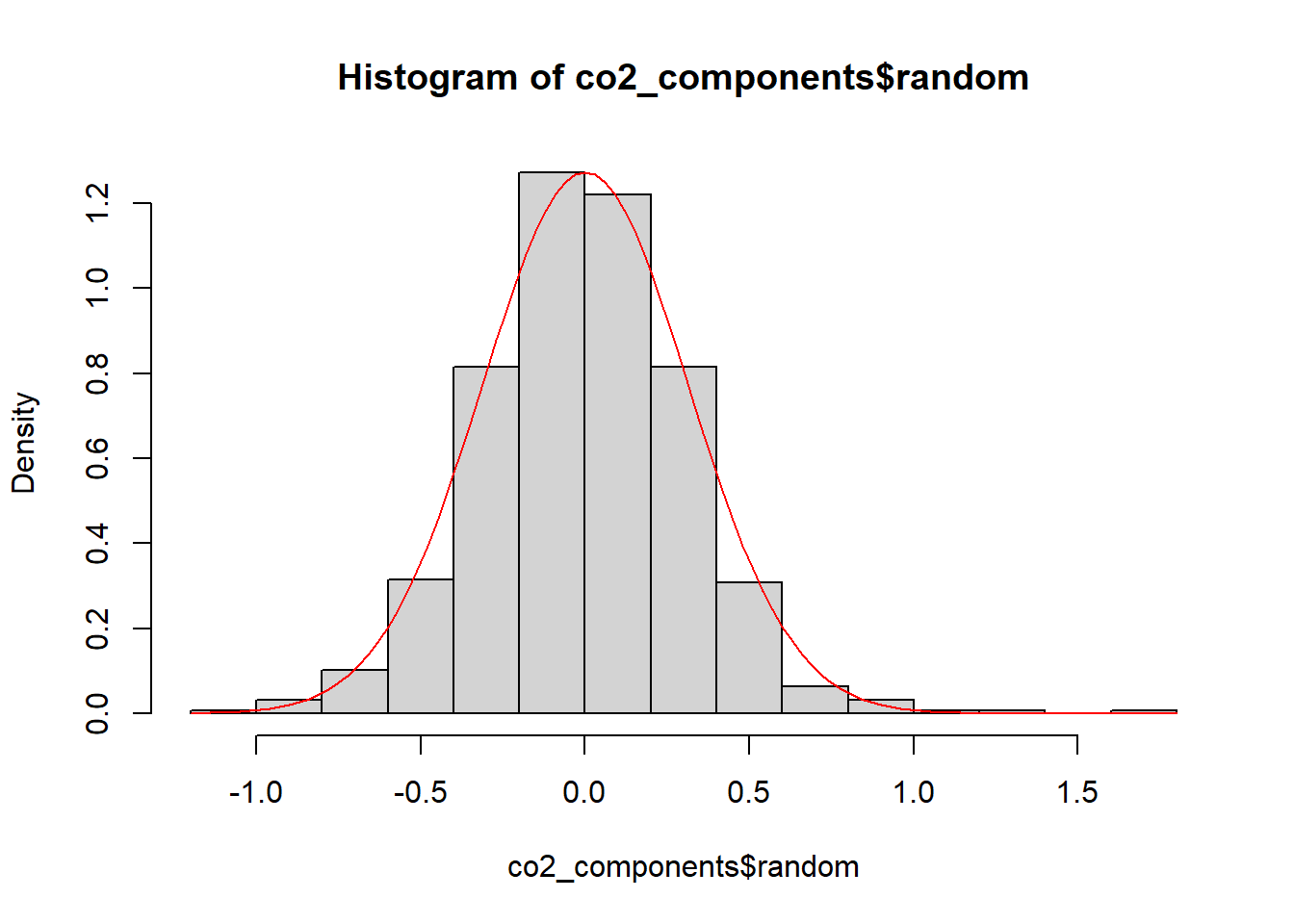

As you can see the distribution is a Gaussian white noise, which is a particularly useful white noise series.

This section is based on the chapters of Time Series Analysis and Its Applications With R Example by Robert H. Shumway and David S. Stoffer.

ARIMA modeling

ARIMA is the abbreviation for AutoRegressive Integrated Moving Average. Auto Regressive (AR) terms refer to the lags of the differenced series, Moving Average (MA) terms refer to the lags of errors and I is the number of difference used to make the time series stationary.

Here stationary actually refers weakly stationary time series, which is a finite variance process such that:

  • The mean value of time-series is constant over time

  • The autovariance function does not change over time

  • Seasonality effect is minimal

AR model

Autoregressive models are based on the idea that the current value of the series, \(x_t\), can be explained as a function of p past values, \(x_{t-1}\), \(x_{t-2}\), …, \(x_{t-p}\), where p determines the number of steps into the past needed to forecast the current value.

An autoregressive (AR) model of order p, abbreviated AR(p), is of the form

\[x_t = \phi_1x_{t-1} + \phi_2x_{t-2} + ... + \phi_px_{t-p} + w_t\]

where \(x_t\) is stationary, \(w_t \sim wn(0, \sigma^2_w)\), and \(\phi_1\), \(\phi_2\), …, \(\phi_p\) are constants.

The following R code can be used to obtain two AR(1) models:

# Make two panels
par(mfrow=c(2,1))

# ARIMA model (1,0,0)
plot(arima.sim(list(order=c(1,0,0), ar=.9), n=100), ylab="x",
main=(expression(AR(1)~~~phi==+.9)))

# ARIMA model (1,0,0)
plot(arima.sim(list(order=c(1,0,0), ar=-.9), n=100), ylab="x",
main=(expression(AR(1)~~~phi==-.9)))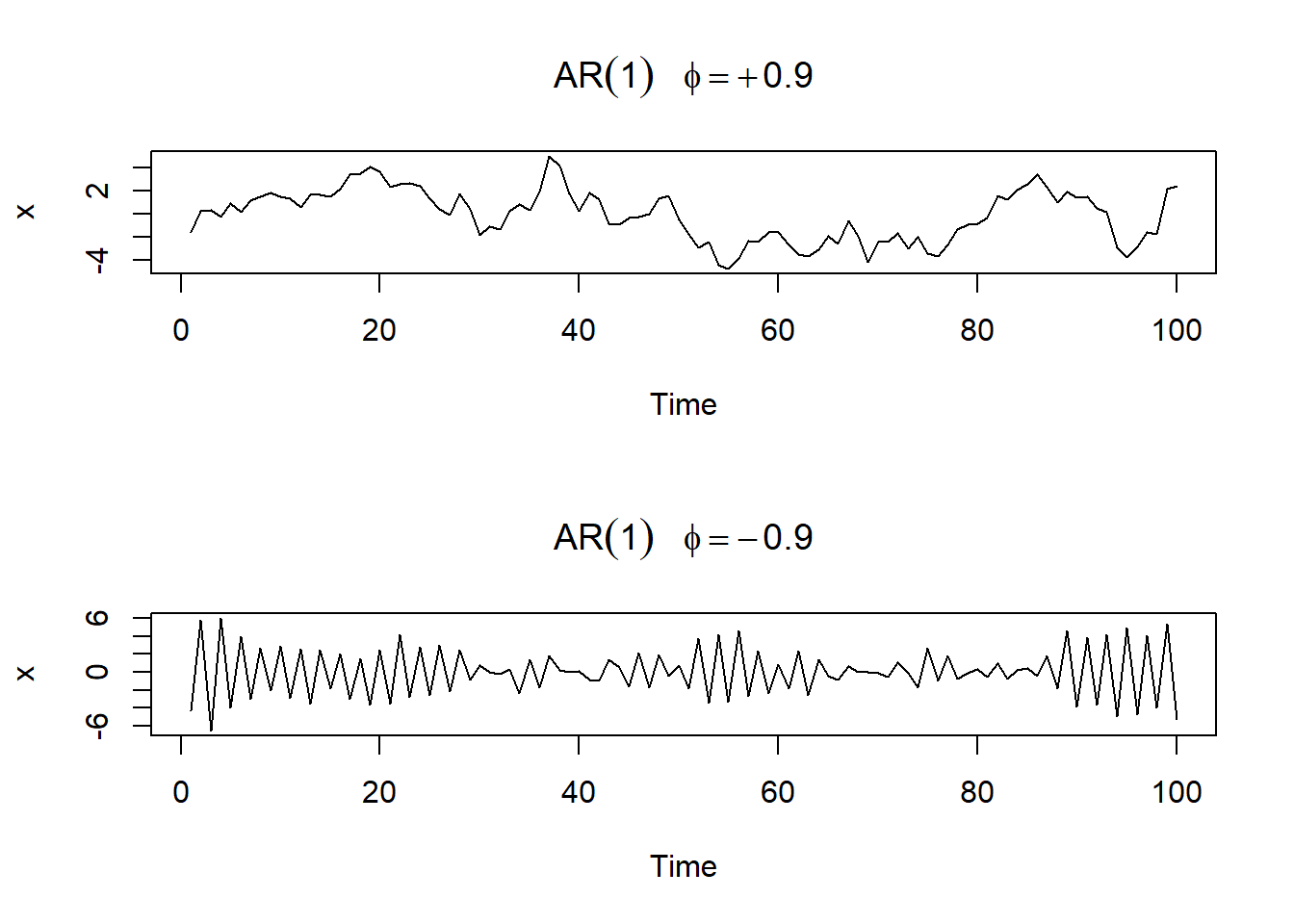

MA model

As an alternative to the autoregressive representation in which the \(x_t\) on the left-hand side of the equation are assumed to be combined linearly, the moving average (MA) model of order q, abbreviated as MA(q), assumes the white noise \(w_t\) on the right-hand side of the defining equation are combined linearly to form the observed data.

The moving average model of order q, or MA(q) model, is defined to be

\[x_t = w_t + \theta_1w_{t-1} + \theta_2w_{t-2} + ... + \theta_qw_{t-q} \]

where \(w_t \sim wn(0, \sigma^2_w)\), and \(\theta_1\), \(\theta_2\), …, \(\theta_q\) are parameters.

The following R code can be used to obtain two MA(1) models:

# Make two panels
par(mfrow=c(2,1))

# ARIMA model (0,0,1)
plot(arima.sim(list(order=c(0,0,1), ma=.9), n=100), ylab="x",
main=(expression(MA(1)~~~theta==+.9)))

# ARIMA model (0,0,1)
plot(arima.sim(list(order=c(0,0,1), ma=-.9), n=100), ylab="x",
main=(expression(MA(1)~~~theta==-.9)))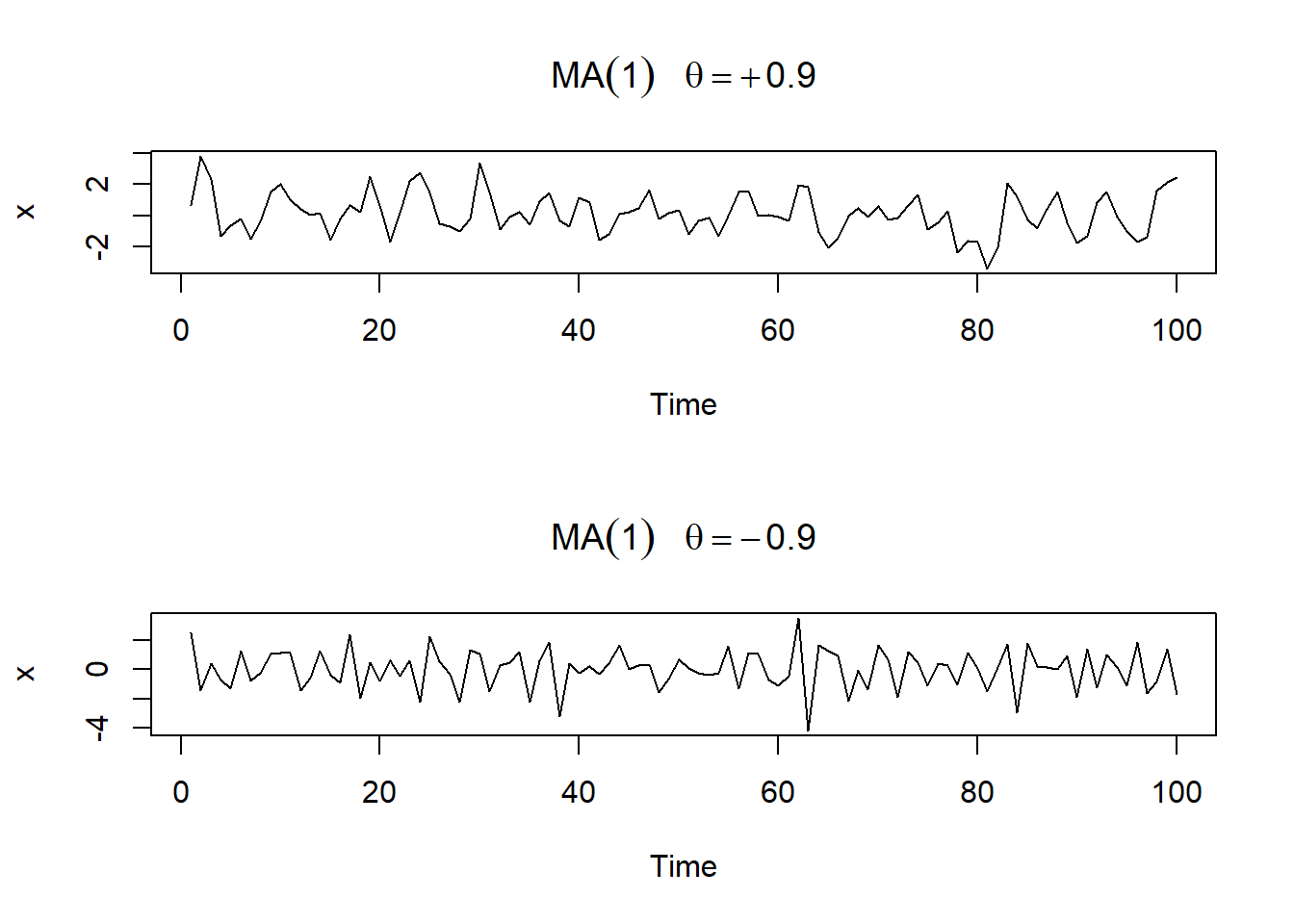

ACF and PACF

The autocorrelation function (ACF) measures the linear predictability of the series at time t, say \(x_t\), using only the value \(x_s\).

The partial auto-correlation function (PACF) is a measure of the correlation between observations of a time series that are separated by k time units (\(x_t\) and \(x_{t-k}\)), with linear dependence removed. In other words, the partial autocorrelation at lag k is the autocorrelation between \(x_t\) and \(x_{t-k}\) that is not accounted for by lags 1 through k−1.

To show ACF and the PACF of a AR model, AR(2), in R we can use the following lines:

# Compute ACF and PACF of AR(2)
ACF = ARMAacf(ar=c(1.5,-.75), ma=0, 24)[-1]
PACF = ARMAacf(ar=c(1.5,-.75), ma=0, 24, pacf=TRUE)

# Plot ACF and PACF of AR(2)
par(mfrow=c(1,2))
plot(ACF, type="h", xlab="lag", ylim=c(-.8,1)); abline(h=0)
plot(PACF, type="h", xlab="lag", ylim=c(-.8,1)); abline(h=0)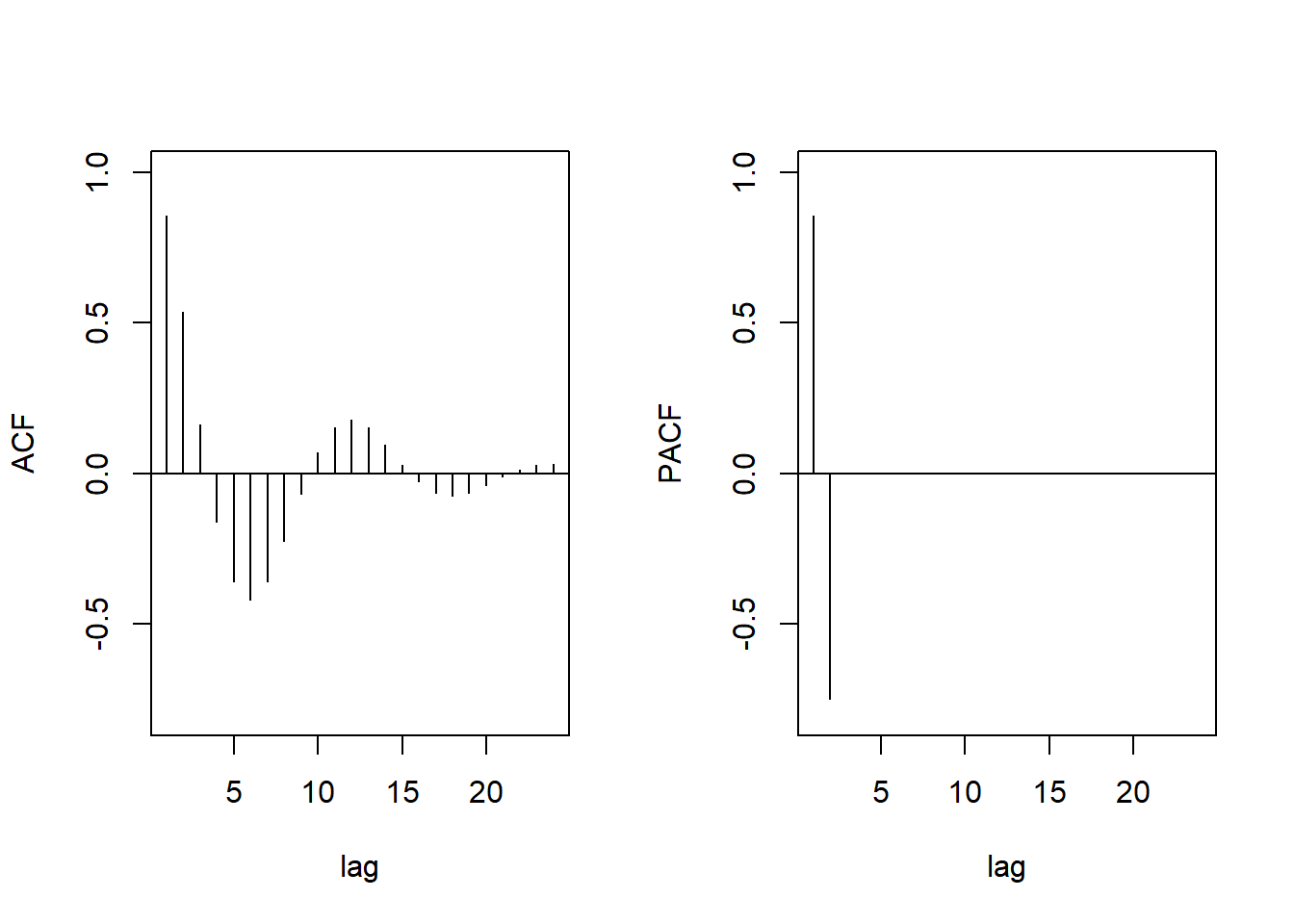

To show ACF and the PACF of a MA model, MA(2), in R we can use the following lines:

# Compute ACF and PACF of MA(2)
ACF = ARMAacf(ar=0, ma=c(0.5,0.6), 24)[-1]
PACF = ARMAacf(ar=0, ma=c(0.5,0.6), 24, pacf=TRUE)

# Plot ACF and PACF of MA(2)
par(mfrow=c(1,2))
plot(ACF, type="h", xlab="lag", ylim=c(-.8,1)); abline(h=0)
plot(PACF, type="h", xlab="lag", ylim=c(-.8,1)); abline(h=0)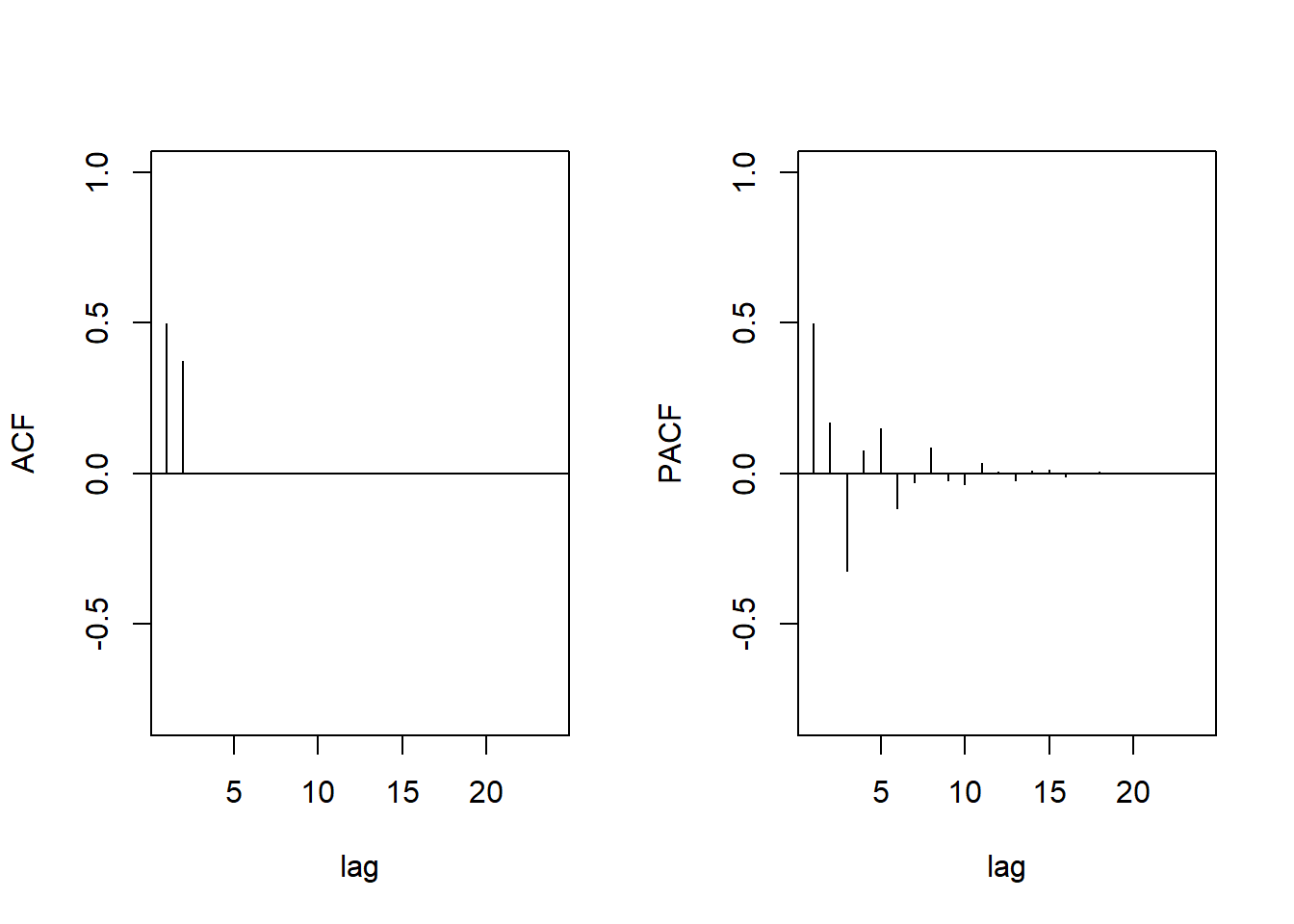

Behavior of the ACF and PACF for ARMA Models can be summarized as:

  • AR(p): ACF Tails off; PACF Cuts off after lag p

  • MA(q): ACF Cuts off after lag q; PACF Tails off

  • ARMA(p, q): ACF Tails off; PACF Tails off

An example

Consider the global temperature series record (gtemp_both) in the astsa package. The data are the global mean land and ocean temperature index from 1850 to 2023. We want to fit an ARIMA model to this time series.

# Load data
library(astsa)
## Warning: 程辑包'astsa'是用R版本4.3.2 来建造的
# Reset panel
par(mfrow=c(1,1))

# Plot
plot(gtemp_both, type="l", ylab="Global Temperature Deviations")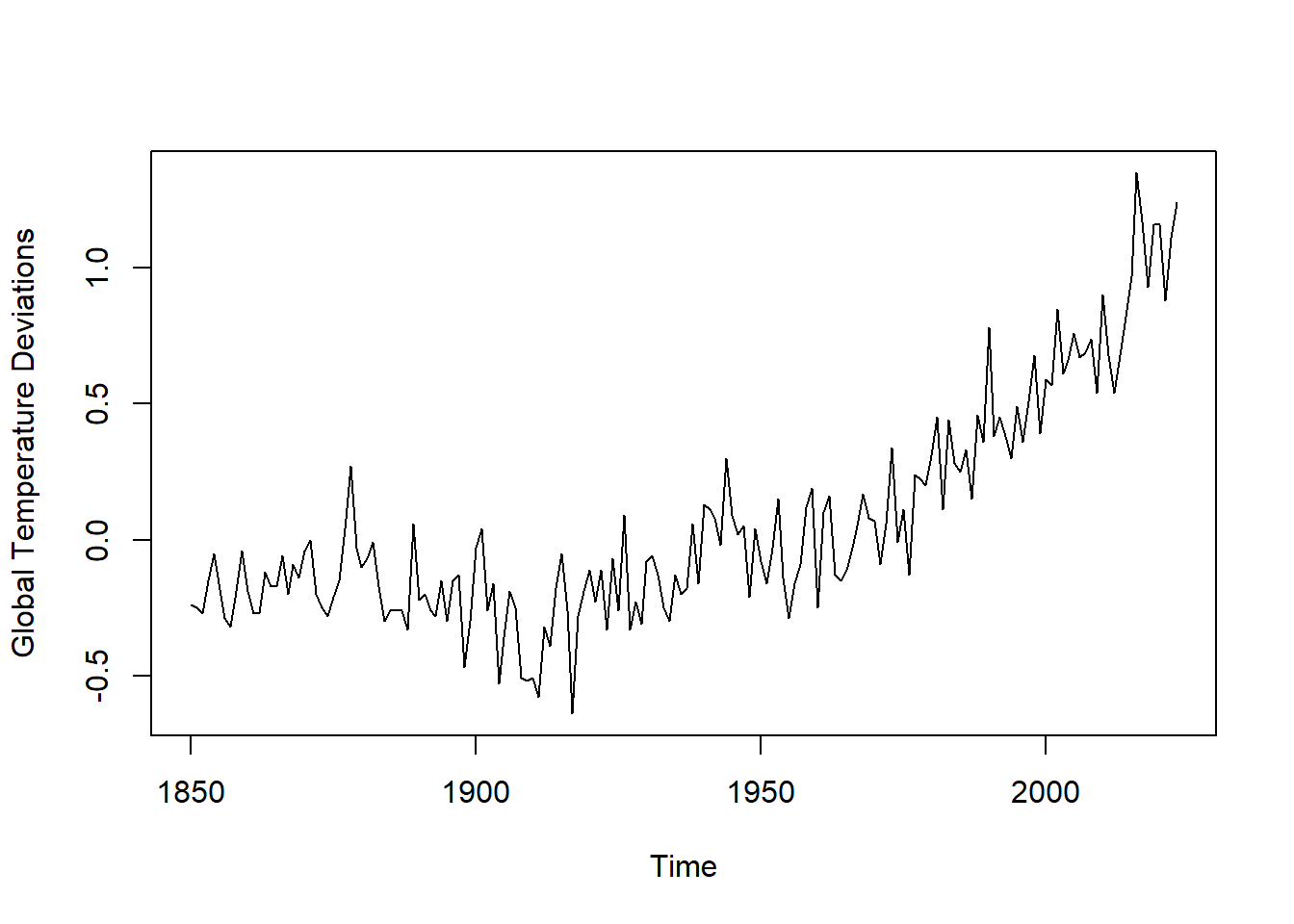

There is a clear trend, so the first step is to de-trend the data.

# Fit a linear model
trModel <- lm(gtemp_both ~ c(1:length(gtemp_both)))

# Get the residuals
residual <- resid(trModel)

# Plot the residual
plot(residual, type="l")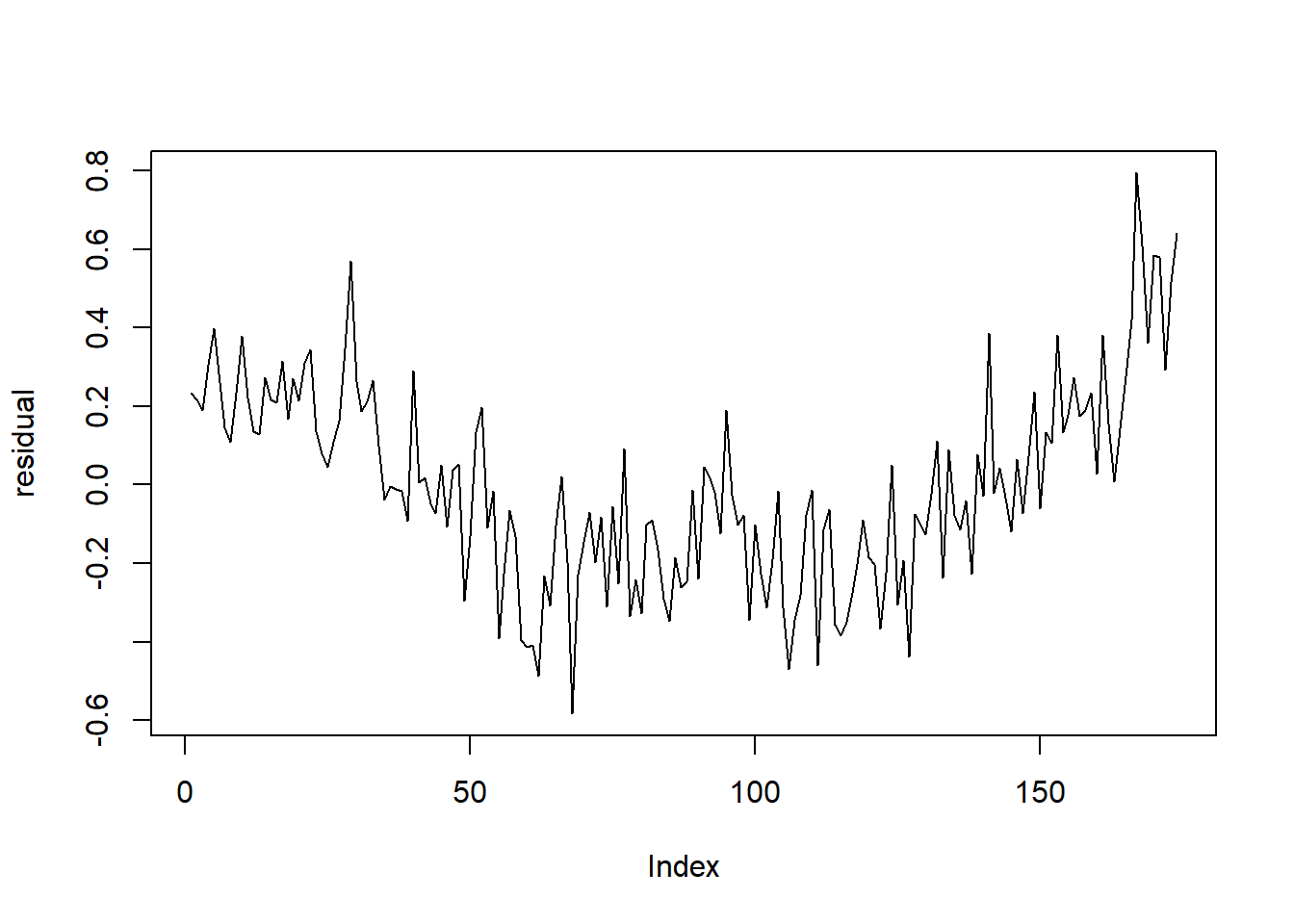

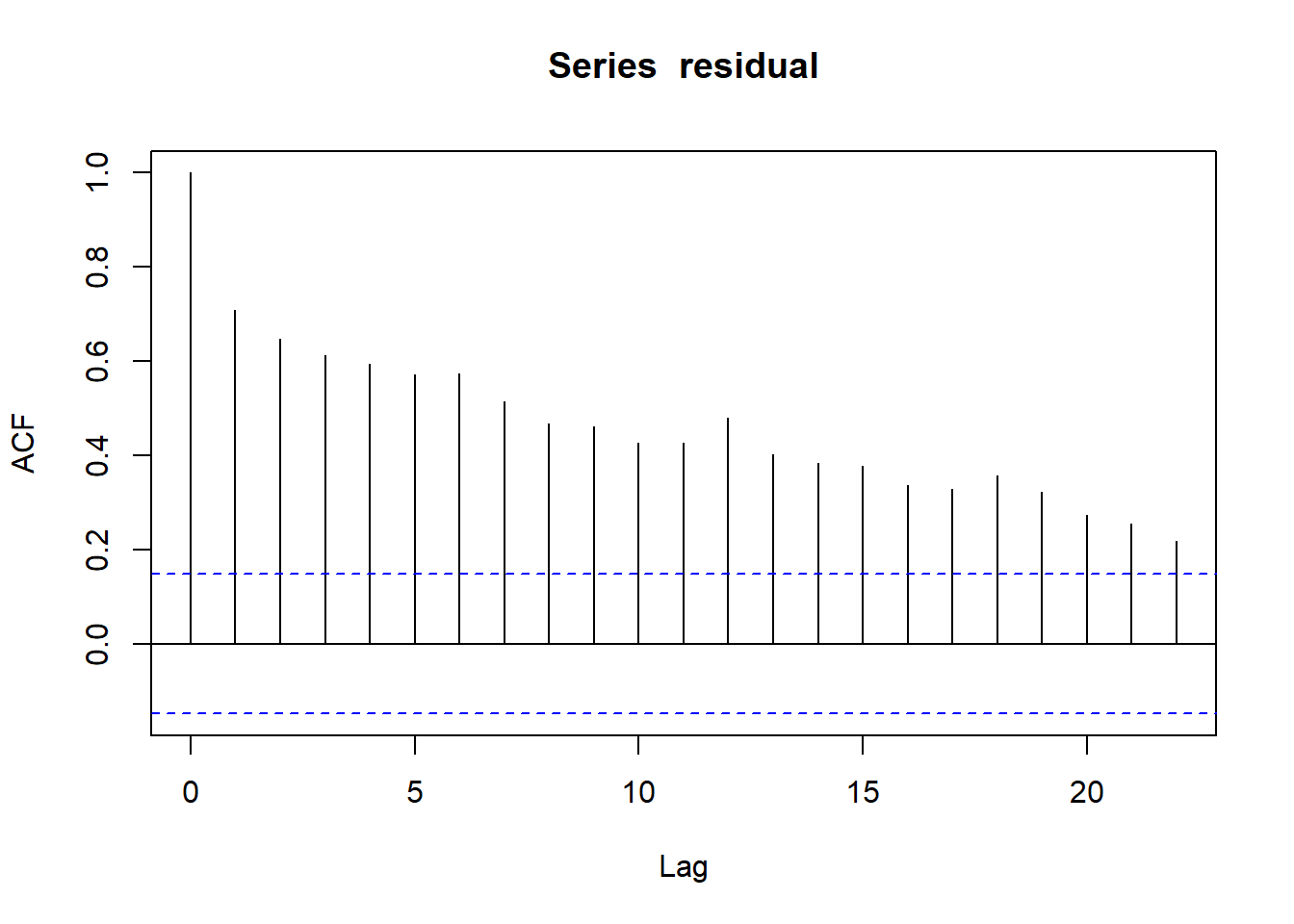
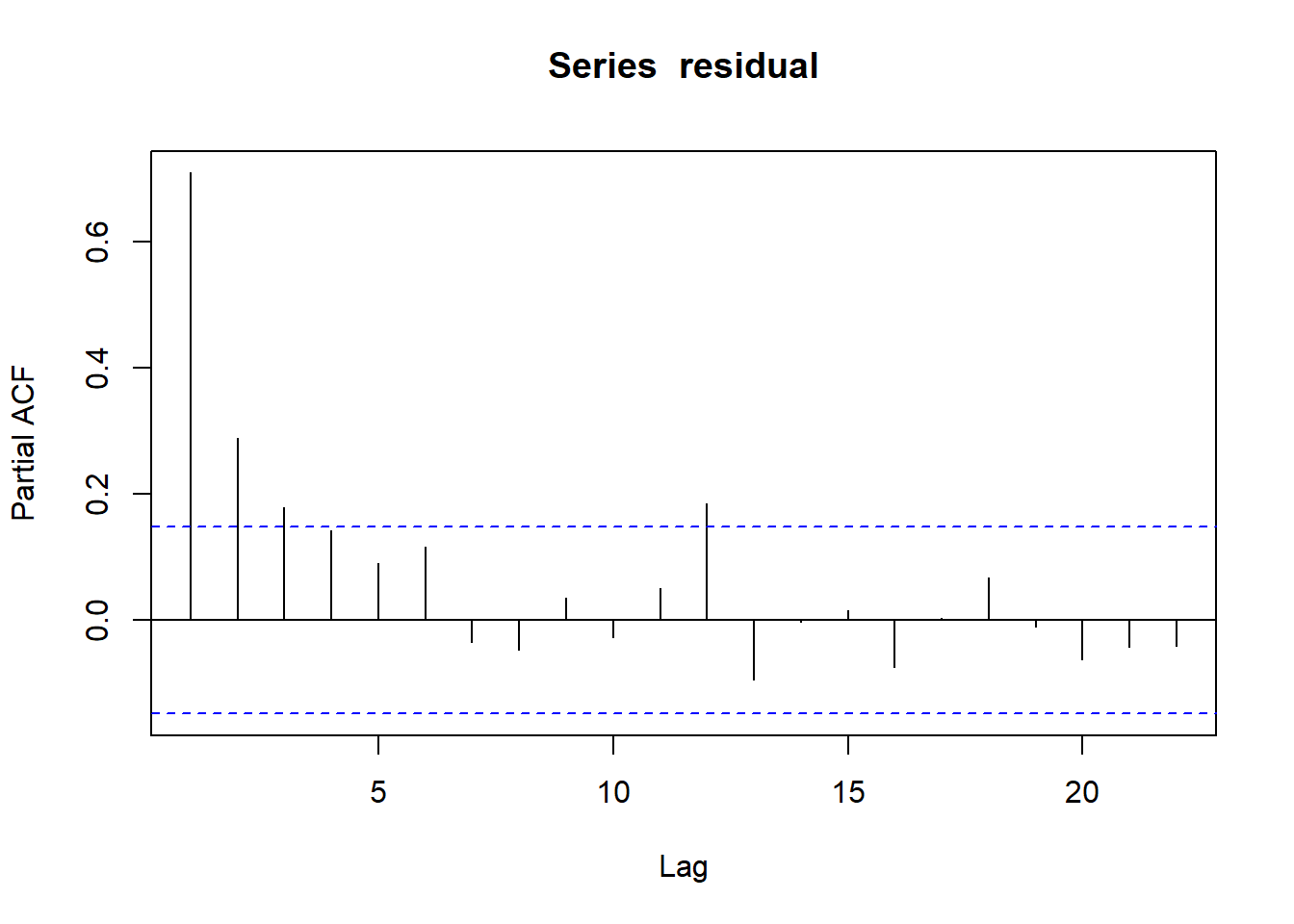
# Check acf anf pacf of the residuals
acf(residual)

pacf(residual)

Based on the acf and pacf plots, we guess it may be an ARMA(3,0) model.

In-class exercises

Exercise #1

Use the data of the Southern Oscillation Index (SOI; soi) data from the astsa package.

  • Practice the decompose() function.

  • Build an ARMA model [Hint: you may want to de-seasonalize the data before fitting the model]