Prerequisites

Load the libraries with R:

library(BSDA)
## Warning: 程辑包'BSDA'是用R版本4.3.3 来建造的
## 载入需要的程辑包：lattice
## 
## 载入程辑包：'BSDA'
## The following object is masked from 'package:datasets':
## 
##     Orange
library(ggplot2)
library(FSA)
## Warning: 程辑包'FSA'是用R版本4.3.3 来建造的
## Registered S3 methods overwritten by 'FSA':
##   method       from
##   confint.boot car 
##   hist.boot    car
## ## FSA v0.9.5. See citation('FSA') if used in publication.
## ## Run fishR() for related website and fishR('IFAR') for related book.

Section example: Soil organic matter

Given the following organic matter contents (unit: %) in different soil types, do organic matters differ among soil types?

Soil type Soil organic matter content (%)
A 2.0, 2.8, 3.3, 3.2, 4.4, 3.6, 1.9, 3.3, 2.8, 1.1
B 3.5, 2.8, 3.2, 3.5, 2.3, 2.4, 2.0, 1.6
C 3.3, 3.6, 2.6, 3.1, 3.2, 3.3, 2.9, 3.4, 3.2, 3.2
D 3.2, 3.3, 3.2, 2.9, 3.3, 2.5, 2.6, 2.8
E 2.6, 2.6, 2.9, 2.0, 2.0, 2.1
F 3.1, 2.9, 3.1, 2.5
G 2.6, 2.2, 2.2, 2.5, 1.2, 1.2
H 2.5, 2.4, 3.0, 1.5

Overview of non-parametric tests

A non-parametric test, also known as a distribution-free test, assumes nothing about the underlying distribution (for example, that the data comes from a normal distribution). That’s compared to parametric test, which makes assumptions about a population’s parameters (for example, the mean or standard deviation); When the word “non-parametric” is used in statistics, it doesn’t quite mean that you know nothing about the population. It usually means that you know the population data does not have a normal distribution.

Situations to use non-parametric tests:

  • The underlying distribution is not normal, thus the normality assumption is not valid

  • Data type is nominal (e.g., pass or fail) or ordinal (aka, ranks or start-rating)

  • One or more assumptions of a parametric test have been violated

  • The sample size is too small (less than 6) to run a parametric test

  • Outliers can not be removed

  • Prefer to test for the median rather than the mean (e.g., very skewed distribution)

Non-parametric tests have lower power compared to parametric tests - they often do not reject H0 when they should.

Mann-Whitney U test

The Mann–Whitney U test is also called the Mann–Whitney–Wilcoxon (MWW), Wilcoxon rank-sum test, or Wilcoxon–Mann–Whitney test. It is used to compare the differences between two independent samples when the sample distributions are not normally distributed and the sample sizes are small (n < 30). It is considered to be the non-parametric equivalent to the two-sample independent t-test.

The requirements of using Mann–Whitney U test are:

  • Random and independent samples

  • For maximum accuracy, there better be no ties. But there is a way to handle ties in the test.

In the Mann–Whitney U test, we have:

  • H0: There is no difference in the two population means

  • H1: There is a difference in the two population means

The Mann–Whitney U test is done with the wilcox.test() function in R:

# Make up samples
Treat     <- c(3, 5, 1, 4, 3, 5)
Control   <- c(4, 8, 6, 2, 1, 9)

# Perform the Mann Whitney U test
wilcox.test(Treat, Control, paired=F, alternative="two.sided")
## Warning in wilcox.test.default(Treat, Control, paired = F, alternative = "two.sided"): 无法精確計算带连结的p值
## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  Treat and Control
## W = 13, p-value = 0.468
## alternative hypothesis: true location shift is not equal to 0

Wilcoxon signed rank test

The Wilcoxon signed rank test is a non-parametric alternative to paired t-test used to compare paired data. It’s used whendata are not normally distributed.

The requirements of using the Wilcoxon signed rank test are:

  • Random and independent samples

  • Approximately symmetrical distributions

In the Wilcoxon signed rank test, we have:

  • H0: There is no difference in the two population means

  • H1: There is a difference in the two population means

The Wilcoxon signed rank test is also done with the wilcox.test() function in R, but with different keywords:

# Make up samples
Treat     <- c(3, 5, 1, 4, 3, 5)
Control   <- c(4, 8, 6, 2, 1, 9)

# Perform the Wilcoxon signed rank test
wilcox.test(Treat, Control, paired=T, alternative="two.sided")
## Warning in wilcox.test.default(Treat, Control, paired = T, alternative = "two.sided"): 无法精確計算带连结的p值
## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  Treat and Control
## V = 5, p-value = 0.2932
## alternative hypothesis: true location shift is not equal to 0

Sign test

When the distribution of differences between paired data values is neither normal nor symmetrical, use the sign test. The sign test is done with the SIGN.test() function from the BSDA package R:

SIGN.test(Treat, Control, alternative = "two.sided", conf.level = 0.95)
## 
##  Dependent-samples Sign-Test
## 
## data:  Treat and Control
## S = 2, p-value = 0.6875
## alternative hypothesis: true median difference is not equal to 0
## 95 percent confidence interval:
##  -4.9  2.0
## sample estimates:
## median of x-y 
##            -2 
## 
## Achieved and Interpolated Confidence Intervals: 
## 
##                   Conf.Level L.E.pt U.E.pt
## Lower Achieved CI     0.7812   -4.0      2
## Interpolated CI       0.9500   -4.9      2
## Upper Achieved CI     0.9688   -5.0      2

Kruskal–Wallis test

The Kruskal–Wallis test, also known as Kruskal–Wallis H test or one-way ANOVA on ranks, is an alternative for the one-way analysis of variance (ANOVA). The test is for checking whether samples originate from the same distribution. It is used for comparing two or more independent samples. It extends the Mann–Whitney U test, which is used for comparing only two groups.

The test assumes that the observations are independent. That is, it is not appropriate for paired observations or repeated measures data.

In the Kruskal–Wallis test, we have:

  • H0: There is no difference among population means

  • H1: There is a difference among population means

The Kruskal–Wallis test is done with the kruskal.test() function in R:

# Load data
require(graphics)

# Boxplots
ggplot(airquality, aes(x=Month, y=Ozone, group=Month, fill=Month)) +
  geom_boxplot() +
  labs(title="Monthly ozone", 
       x="Month", y="Ozone [ppb]") +
  theme_classic()
## Warning: Removed 37 rows containing non-finite values (`stat_boxplot()`).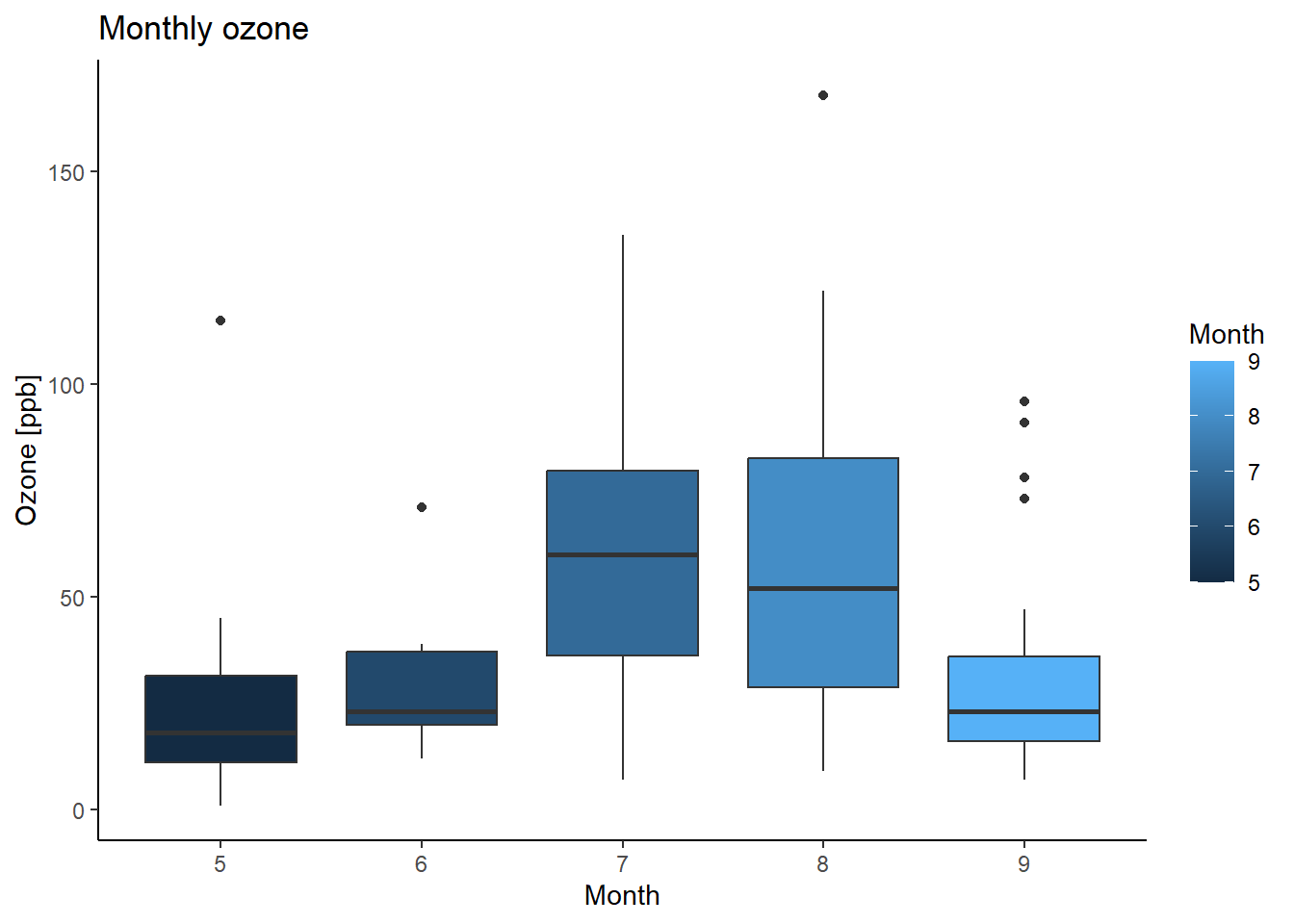

# Perform the Kruskal–Wallis test
kruskal.test(Ozone ~ Month, data = airquality)
## 
##  Kruskal-Wallis rank sum test
## 
## data:  Ozone by Month
## Kruskal-Wallis chi-squared = 29.267, df = 4, p-value = 6.901e-06

The outcome of the Kruskal–Wallis test tells you if there are differences among the group means, but doesn’t tell you which groups are different from other groups. To determine which groups are different from others, post-hoc testing can be conducted. The most common post-hoc test for the Kruskal–Wallis test is the Dunn test, here conducted with the dunnTest() function in the FSA package.

dunnTest(Ozone ~ Month, data=airquality, method="bh")      
## Warning: Month was coerced to a factor.
## Warning: Some rows deleted from 'x' and 'g' because missing data.
## Dunn (1964) Kruskal-Wallis multiple comparison
##   p-values adjusted with the Benjamini-Hochberg method.
##    Comparison            Z      P.unadj        P.adj
## 1       5 - 6 -0.925158616 3.548834e-01 4.436043e-01
## 2       5 - 7 -4.419470641 9.894296e-06 9.894296e-05
## 3       6 - 7 -2.244208032 2.481902e-02 4.963804e-02
## 4       5 - 8 -4.132813422 3.583496e-05 1.791748e-04
## 5       6 - 8 -2.038635487 4.148642e-02 6.914403e-02
## 6       7 - 8  0.286657218 7.743748e-01 8.604164e-01
## 7       5 - 9 -1.321202283 1.864339e-01 2.663342e-01
## 8       6 - 9  0.002538555 9.979745e-01 9.979745e-01
## 9       7 - 9  3.217199124 1.294487e-03 4.314957e-03
## 10      8 - 9  2.922827778 3.468683e-03 8.671708e-03

Spearman correlation test

The Spearman correlation test is a rank-based test that does not require assumptions about the distribution of the data. The correlation coefficient from the test, \(\rho\), ranges from -1 to –1, with +1 being a perfect positive correlation and –1 being a perfect negative correlation. A \(\rho\) of 0 represents no correlation.

In the Spearman correlation test, we have:

  • H0: The populations do not correlate with each other

  • H1: The populations correlate with each other

The Spearman correlation is done with the cor.test() function in R:

# Make up some random values
x <- rnorm(20,0,1)
y <- 2*x+rnorm(20,0,0.5)

# Perform the Spearman correlation test
cor.test(x, y, method="spearman", alternative="two.sided", conf.level=0.95)
## 
##  Spearman's rank correlation rho
## 
## data:  x and y
## S = 76, p-value = 5.785e-06
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##       rho 
## 0.9428571

Kendall correlation test

The Kendall correlation test is also a rank-based test. The correlation coefficient from the test is \(\tau\), ranging from -1 to +1.

Used the Kendall correlation when the sample size is small or there are many tied ranks.

In the Kendall correlation test, we have:

  • H0: The populations do not correlate with each other

  • H1: The populations correlate with each other

The Kendall correlation is also done with the cor.test() function in R:

# Perform the Kendall correlation test
cor.test(x, y, method="kendall", alternative="two.sided", conf.level=0.95)
## 
##  Kendall's rank correlation tau
## 
## data:  x and y
## T = 172, p-value = 9.061e-09
## alternative hypothesis: true tau is not equal to 0
## sample estimates:
##       tau 
## 0.8105263

Summary of non-parametric tests

Purpose Parametric Alternative non-parametric
Checking independence Runs test
Checking normality Shapiro-Wilk test, Lillifors test
Checking Outliers Grubbs’ test, Dixon’s test, Rosner’s test Walsh’s test
Comparing means of two independent populations t test Mann-Whitney U test
Comparing means of two paired populations paired t test Wilcoxon signed rank, Signed test
Comparing means of more than 2 independent populations One-way ANOVA Kruskal–Wallis test
Checking correlation Pearson test Spearman test, Kendall test

In-class exercises

Exercise #1

Using data from the section example, do organic matters differ among soil types? Report your results.