Assignment 01
Out: 10/15 19:00
Due: 10/29 19:00
Instructions
Collaboration:
Collaboration on solving the assignment is allowed, after you have thought about the problem sets on your own. It is also OK to get clarification (but not solutions) from online resources, again after you have thought about the problem sets on your own.
There are two requirements about collaboration:
Cite your collaborators fully and completely (e.g., “XXX explained to me what is asked in problem set 3”). Or cite online resources (e.g., “I got inspired by reading XXX”) that helped you.
Write your scripts and report independently - the scripts and report must come from you only.
Submitting your assignment:
Please write a report
PS1.pdf.Create a jupyter notebook named
PS1.ipynb.Upload your jupyter notebook and report to your Github
ESE5023_Assignments_XXXrepository (whereXXXis your SUSTech ID) before the due time.
Late Submission:
Late submissions will not receive any credit. The submission time will be determined based on your latest GitHub file records.
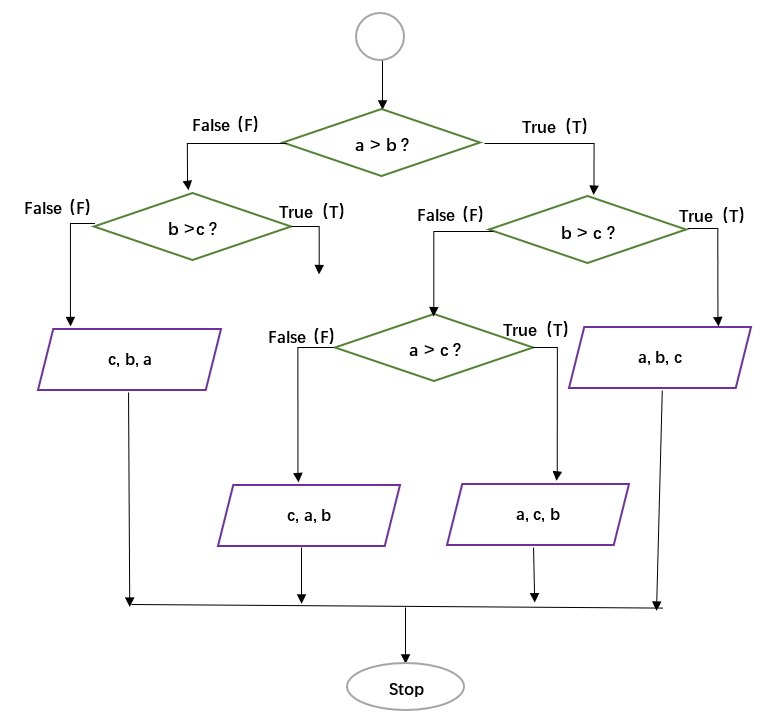
1. Flowchart
[10 points] Write a function
Print_values with arguments a, b,
and c to reflect the following flowchart. Here the purple
parallelogram operator on a list [x, y, z] is to compute
and print x+y-10z. Try your output with some random
a, b, and c values. Report your
output when a = 5, b = 15, c = 10.
2. Continuous celing function
[10 points] Given a list with N
positive integers. For every element x of the list, find
the value of continuous ceiling function defined as
F(x) = F(ceil(x/3)) + 2x, where F(1) = 1.
3. Dice rolling
3.1 [15 points] Given 10 dice each with
6 faces, numbered from 1 to 6.
Write a function Find_number_of_ways to find the number of
ways to get sum x, defined as the sum of values on each
face when all the dice are thrown.
3.2 [5 points] Count the number of ways for any
x from 10 to 60, assign the
number of ways to a list called Number_of_ways, so which
x yields the maximum of Number_of_ways?
4. Dynamic programming
4.1 [5 points] Write a function
Random_integer to fill an array of N elements
by randomly selecting integers from 0 to
10.
4.2 [15 points] Write a function
Sum_averages to compute the sum of the average of all
subsets of the array. For example, given an array of
[1, 2, 3], you Sum_averages function should
compute the sum of: average of [1], average of
[2], average of [3], average of
[1, 2], average of [1, 3], average of
[2, 3], and average of [1, 2, 3].
4.3 [5 points] Call Sum_averages with
N increasing from 1 to 100,
assign the output to a list called Total_sum_averages. Plot
Total_sum_averages, describe what do you see.
5. Path counting
5.1 [5 points] Create a matrix with N
rows and M columns, fill the right-bottom corner and
top-left corner cells with 1, and randomly fill the rest of
matrix with integer 0 or 1.
5.2 [25 points] Consider a cell marked with
0 as a blockage or dead-end, and a cell marked with
1 is good to go. Write a function Count_path
to count total number of paths to reach the right-bottom corner cell
from the top-left corner cell.
Notice: for a given cell, you are only allowed to move either rightward or downward.
5.3 [5 points] Let N = 10, M = 8, run
Count_path for 1000 times, each time the
matrix (except the right-bottom corner and top-left corner cells, which
remain being 1) is re-filled with integer 0 or
1 randomly, report the mean of total number of paths from
the 1000 runs.