“NumPy is the reason why Python stands among the ranks of R, Matlab, and Julia, as one of the most popular languages for doing STEM-related computing.” - Python like you mean it

Introduction to numPy

numPy is a third-party library that facilitates numerical computing in Python by providing users with a versatile N-dimensional array object for storing data, and powerful mathematical functions for operating on those arrays of numbers. NumPy implements its features in ways that are highly optimized, via a process known as vectorization, that enables a degree of computational efficiency that is otherwise undoable by the Python language.

Import numPy

numPy should be installed along with Anaconda. To import it, run:

# import numpy 
import numpy as np

Here we use np as an alias (a.k.a., a nickname) of numPy, and later use it heavily. You can check functions and variables in a module (I will use the term “module”, some people prefer “package” or “library”) with the dir() function.

# Check functions and variables contained in a module
dir(np)

N-dimensional array (ndarray)

NumPy is used to work with arrays. The array object in NumPy is called ndarray. We can create a ndarray object by using the array() function:

# Create an array from a list
arr = np.array([1, 2, 3, 4, 5, 6])

# Check the object
type(arr)

# Check the shape
np.shape(arr)

Every numpy array is a grid of elements of the same type. Numpy provides a large set of numeric datatypes that you can use to construct arrays. Numpy tries to guess a datatype when you create an array, but functions that construct arrays usually also include an optional argument to explicitly specify the datatype. For example:

x = np.array([1, 2])
print(x.dtype) 

y = np.array([1.0, 2.0]) 
print(y.dtype) 

# Force a particular datatype
z = np.array([1, 2], dtype=np.int64)   
print(z.dtype)

For more about numpy datatypes, check Data type objects.

You can also create arrays on various dimensions:

# 0-D
arr0 = np.array(1)
print(arr0) 

# 1-D
arr1 = np.array([1, 2, 3, 4, 5, 6])
print(arr1) 

# 2-D
arr2 = np.array([[1, 2, 3], [4, 5, 6]])
print(arr2) 

# 3-D
arr3 = np.array([[[1, 2, 3], [4, 5, 6]], [[1, 2, 3], [4, 5, 6]]])
print(arr3) 

# Use ndim to verify the dimensions
print(arr0.ndim)
print(arr1.ndim)
print(arr2.ndim)
print(arr3.ndim)

Reshaping

Reshaping means changing the shape of an array. The shape of an array is the number of elements in each dimension. By reshaping, we can add or remove dimensions or change number of elements in each dimension.

arr4 = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])

# 1-D to 2-D
print(arr4.reshape(4, 3))

# 1-D to 3-D
print(arr4.reshape(2, 2, 3))

# This will return an error
print(arr4.reshape(2, 3, 4))

# This is fine, -1 means "unknown" dimension, python will compute it for you.
print(arr4.reshape(2, 3, -1))

Array creation

There are some built-in functions to create arrays, check the following lines:

# Create some uniform arrays
a1 = np.zeros((2,2))
print(a1)

a2 = np.full((3,3), np.pi)
print(a2)

a3 = np.ones_like(a1)
print(a3)

a4 = np.zeros_like(a2)
print(a4)

You can create an array in a defined range:

# create some ranges
a5 = np.arange(10)
print(a5)

# arange is left inclusive, right exclusive
a6 = np.arange(0,3,0.25)
print(a6)

# linearly spaced
a7 = np.linspace(10,100,10)
print(a7)

# log spaced
a8 = np.logspace(1,2,10)
print(a8)

Indexing and slicing

Array indexing and slicing are the same as accessing a list element. Remember, index starts from 0:

# indexing
print(arr2[0,0])
print(arr2[0,-1])
print(arr2[-1,-1])

One thing new is integer array indexing:

# Make up an array
a = np.linspace(1,12,12).reshape(3,4)
print(a)

# integer array indexing: [0,2] and [1,0]
print(a[[0, 1], [2, 0]]) 

# integer array indexing: [0,2], [1,0], [-1,-1], and [2,2]
print(a[[0, 1, -1, 2], [2, 0, -1, 2]]) 

# one step more, change the array
# can you figure out why
b = [0, 1, 2]
print(a)
a[np.arange(3), b] += 100
print(a)

You can also use boolean indexing:

# Make up an array
a = np.linspace(1,12,12).reshape(3,4)
print(a)

# Find the elements of a that are bigger than 5
index_b = a > 5
print(index_b)
print(a[index_b])

# or simply
print(a[a>5])

Array operations: basic math

Basic mathematical functions operate elementwise on arrays, and are available both as operator overloads and as functions in the numpy module:

# Make up two arrays
x = np.array([[1,2],[3,4]], dtype=np.float64)
y = np.array([[5,6],[7,8]], dtype=np.float64)

# Elementwise operator; both produce the array
print(x + y)
print(np.add(x, y))

# Difference
print(x - y)
print(np.subtract(x, y))

# Product
print(x * y)
print(np.multiply(x, y))

# Division
print(x / y)
print(np.divide(x, y))

# Square root
print(np.sqrt(x))

Please check Mathematical functions for a list of all available functions in numpy.

Array operations: matrix

Numpy uses the dot function to compute inner products of vectors, to multiply a vector by a matrix, and to multiply matrices. dot is available both as a function in the numpy module and as an instance method of array objects. For example:

# Make up two arrays
x1 = np.array([[1,2],[3,4]])
x2 = np.array([[5,6],[7,8]])

# Make up two more arrays
y1 = np.array([9,10])
y2 = np.array([11, 12])

# Inner product of vectors
print(y1.dot(y2))
print(np.dot(y1, y2))

# Matrix product
print(x1.dot(y1))
print(np.dot(x1, y1))

# Matrix product
print(x1.dot(x2))
print(np.dot(x1, x2))

To transpose a matrix, simply use the T attribute of an array object:

print(x1)
print(x1.T)

Array operations: statistics

Numpy also provides a range of functions to compute statistics of an array. For example:

x = np.linspace(1,12,12).reshape(4,3)

# Get the sum
np.sum(x)

# Get the sum along an axis, make sure you understand
np.sum(x, axis=0) 
np.sum(x, axis=1) 

# Get the max and min along an axis
np.amax(x) 
np.amax(x, axis=0)

This figure shows the concept of “axis”

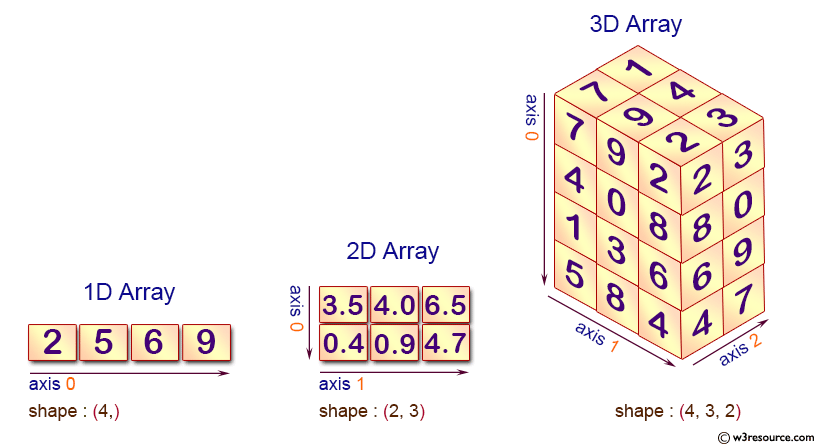
drawing

Please check Statistics functions for a list of all available functions in numpy.

Broadcasting

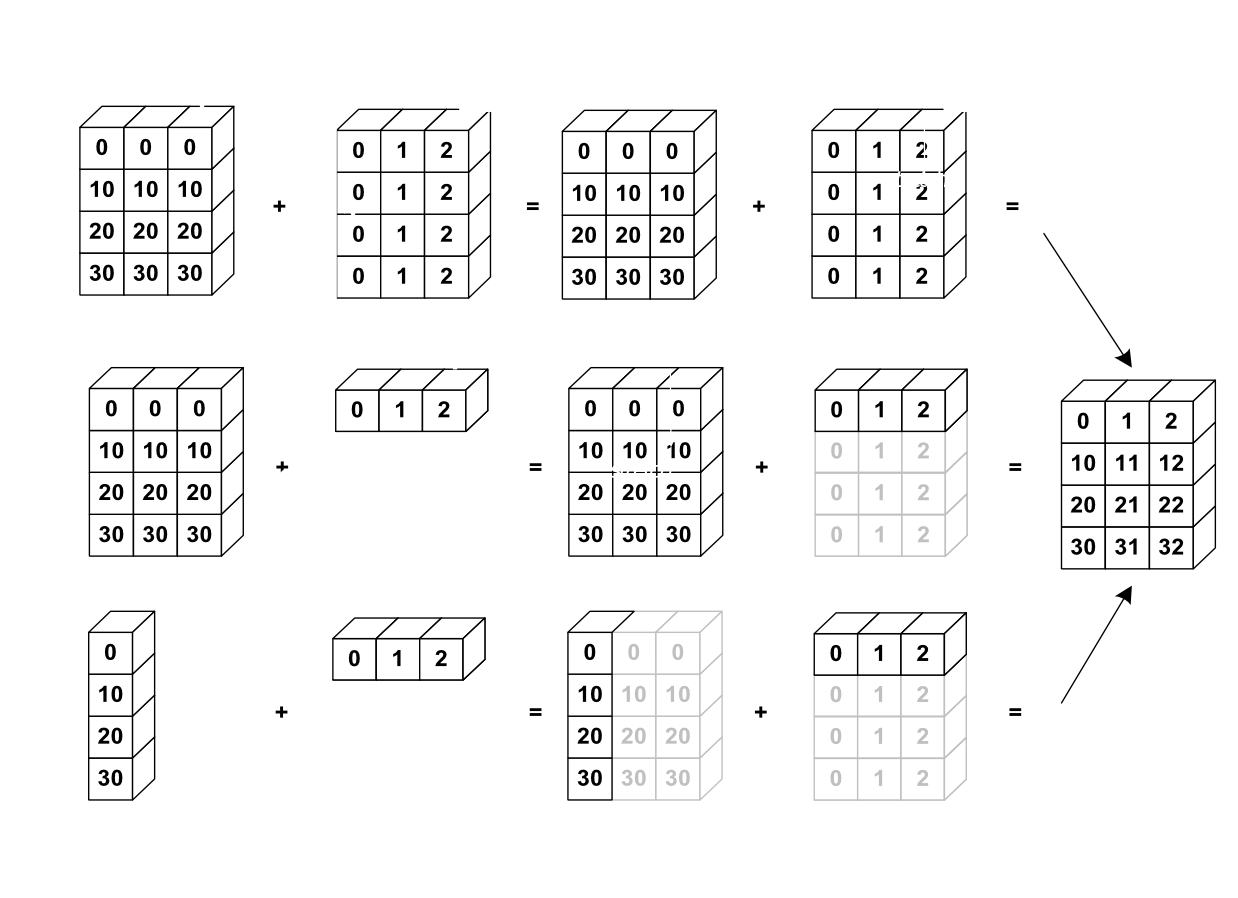
drawing

The term broadcasting describes how numpy treats arrays with different shapes during arithmetic operations. Subject to certain constraints, the smaller array is “broadcast” across the larger array so that they have compatible shapes. Broadcasting usually leads to efficient algorithm implementations.

When operating on two arrays, NumPy compares their shapes element-wise. It starts with the trailing (i.e. rightmost) dimensions and works its way left. Two dimensions are compatible when:

  • they are equal, or

  • one of them is 1

If these conditions are not met, a ValueError: operands could not be broadcast together exception is thrown, indicating that the arrays have incompatible shapes. The size of the resulting array is the size that is not 1 along each axis of the inputs.

# 4*3 array
x = np.array([[0,0,0], [10,10,10], [20,20,20], [30,30,30]])
print(x)

# 1*3 array
v = np.array([0, 1, 2])
print(v)

# 4*3 and 1*3 is compatible
# Add v to each row of x using broadcasting
y = x + v 
print(y) 

# 3*1 and 1*3 is compatible
x = x[:,0]
x = x[:, np.newaxis]
print(x)
v = np.array([0, 1, 2])
print(v)
y = x + v  # Add v to each row of x using broadcasting
print(y)

Please check this for more about broadcasting.

Joining Array

Joining means putting the contents of two or more arrays in a single array. NumPy joins arrays by axes - we pass a sequence of arrays that we want to join to the concatenate() function, along with the axis. If the axis is not explicitly passed, it is taken as 0. For example:

# Joining 1-D arrays
arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
arr = np.concatenate((arr1, arr2))
print(arr) 

# Joining 2-D arrays
arr1 = np.array([[1, 2], [3, 4]])
arr2 = np.array([[5, 6], [7, 8]])
arr = np.concatenate((arr1, arr2), axis=1)
print(arr)

Similar to concatenate(), hstack(), vstack(), and dstack() can also join arrays. Try those for yourself.

In-class exercises

Exercise #1

Create an array as follows:

1,  1,  1,  1, 1
1, 99, 99, 99, 1
1, 99, -20, 99, 1
1, 99, 99, 99, 1
1,  1,  1,  1, 1

Exercise #2

Generate a 1-D array of 10 random integers. Each integer should be a number between 30 and 40 (inclusive).

[Hint: use np.random.randint() ]

Exercise #3

Create an array 1,2,3,np.nan,5,6,7,np.nan, replace all nan values with -9999.

[Hint: use isnan() ]

Exercise #4

Create an array with np.random.uniform(1,50,20) (make sure you understand it), then replace all values greater than 30 to 30 and less than 10 to 10.

[Hint: try np.where() function]

Exercise #5

Create an array with np.arange(20), replace all odd numbers in the array with -1.

Exercise #6

Create two arrays (x and y) with np.random.randint(), find elements in x where its value is larger than its corresponding element in y.

[Hint: try np.where() function]

Exercise #7

Run the following lines:

x = np.linspace(1,10,10)
print(x)
y = x
y[1] = -99
print(x)

It’s strange, x also changes even we only changes y. Now try y = np.copy(x) instead of y = x.